Hva er gjennomsnitt? Det er et tall som prøver å beskrive en «typisk» verdi i en gruppe. I matematikk kalles dette ofte middelverdi.
Middelverdi er det samme som det aritmetiske gjennomsnittet. Du finner det ved å ta summen av alle tallene og dele på antall tall.
Du bruker gjennomsnitt hele tiden, selv når du ikke tenker over det. Du møter det i karakterer. Du møter det i værmeldinger. Du møter det i statistikk.
Gjennomsnitt gjør det lettere å forstå store mengder tall.
Men gjennomsnitt er ikke magi. Det er et verktøy. Noen ganger gir det et godt bilde. Andre ganger kan det lure deg litt.
Hovedpunkter
- Gjennomsnitt er middelverdien av flere tall.
- Du regner ut gjennomsnitt ved å summere og dele på antall verdier.
- Gjennomsnitt påvirkes av ekstreme verdier, som høye eller lave tall.
- Median og typetall kan passe bedre i skjeve datasett.
Hva betyr «gjennomsnitt» i matte?
I matte er gjennomsnitt et sentralmål. Sentralmål beskriver hvor «midtpunktet» i et datamateriale ligger. De vanligste sentralmålene er gjennomsnitt, median og typetall.
Gjennomsnitt tar med alle verdiene dine. Det er både styrken og svakheten.
Hvis ett tall endrer seg, endrer gjennomsnittet seg også. Det kan være nyttig når du vil se en samlet utvikling.
Hva brukes gjennomsnitt til?
Gjennomsnitt brukes til å forenkle sammenligning. Du kan sammenligne klasser. Du kan sammenligne lag. Du kan sammenligne måneder. Du slipper å stirre på hundre tall.
Her er typiske situasjoner:
- Karaktergjennomsnitt på vitnemål.
- Gjennomsnittstemperatur i juli.
- Snittpoeng i en liga.
- Gjennomsnittlig reisetid til skolen.
I statistikk brukes gjennomsnitt ofte sammen med andre mål. Grunnen er enkel. To datasett kan ha samme gjennomsnitt, men helt ulik fordeling.
NDLA beskriver nettopp dette poenget når de forklarer sentralmål og spredning.
Hvordan regne gjennomsnitt?
Dette er kjernen. Hvordan regne gjennomsnitt på en trygg måte?
Oppskriften
- Legg sammen alle tallene.
- Del summen på hvor mange tall du har.
Dette er også den vanlige forklaringen i norske læringsressurser. Gjennomsnitt er middelverdi, og du finner den ved å summere og dele på antall data.
Gjennomsnitt = sum av tallene ÷ antall tall
Eksempel 1: Regne ut gjennomsnitt på karakterer
Du har fått disse karakterene:
4, 5, 3, 4, 6
Først finner du summen:
4 + 5 + 3 + 4 + 6 = 22
Så deler du på antall karakterer:
22 ÷ 5 = 4,4
Gjennomsnittet ditt er 4,4.
Dette er et klassisk «regne ut gjennomsnitt»-eksempel. Høyskoler viser samme metode når de forklarer gjennomsnittskarakter.
Eksempel 2: Finne gjennomsnitt for temperaturer
Du noterer temperaturene denne uka:
2, 1, 3, 0, 4, 2, 1
Summen blir:
2 + 1 + 3 + 0 + 4 + 2 + 1 = 13
Du har 7 dager:
13 ÷ 7 = 1,857…
Du kan skrive 1,86 grader. Du kan også runde til 1,9 grader. Runding avhenger av hva du trenger.
Poenget er dette. Du kan finne gjennomsnitt på samme måte, selv når svaret blir et desimaltall.
Hvordan regne ut gjennomsnitt med desimaltall?
Mange tror desimaltall gjør det vanskelig. Det gjør det ikke. Du gjør det samme.
Tallene er:
2,5, 3,0, 4,5
Summen er:
2,5 + 3,0 + 4,5 = 10,0
Del på antall tall:
10,0 ÷ 3 = 3,33 …
Gjennomsnittet er cirka 3,33.
Gjennomsnitt kan bli misvisende hvis ett tall er veldig høyt eller lavt. Da kan median eller typetall gi et mer realistisk bilde av hva som er vanlig.
Vanlige feil når du skal regne ut gjennomsnitt
Dette er feilene vi oftest ser:
- Du deler på feil antall: Du legger sammen fem tall, men deler på fire. Da blir alt feil.
- Du glemmer et tall i summen: Dette skjer ofte når listen er lang. Skriv opp tallene først.
- Du blander gjennomsnitt og median: Gjennomsnitt er en regneoperasjon. Median er midtverdien i sortert liste.
- Du lar ett ekstremt tall styre alt: Dette er ikke en regnefeil. Det er en tolkningsfeil. Den er viktig.
Vil du lære mer om disse, kan du lese egne forklaringer om median her.
Når kan gjennomsnitt gi et misvisende bilde?
Gjennomsnitt påvirkes av ekstreme verdier. Det betyr at ett veldig høyt tall kan dra snittet opp. Ett veldig lavt tall kan dra snittet ned. Dette er grunnen til at man må vurdere hvilket sentralmål som passer.
Eksempel: «typisk» lønn i en liten gruppe
- Fem personer tjener: 350 000, 380 000, 400 000, 420 000, 2 500 000
- Summen er: 350k + 380k + 400k + 420k + 2500k = 4 050 000
- Del på 5: 4 050 000 ÷ 5 = 810 000
Gjennomsnittet blir 810 000 kroner. Det ser høyt ut. Men fire av fem tjener rundt 400 000. Da kan median gi et mer «typisk» bilde.
SSB Skole forklarer at gjennomsnitt, median og typetall brukes nettopp for å beskrive data på ulike måter. De viser også at valget må passe datasettet.
Når tallene er skjevt fordelt, kan gjennomsnittet gi et misvisende bilde.
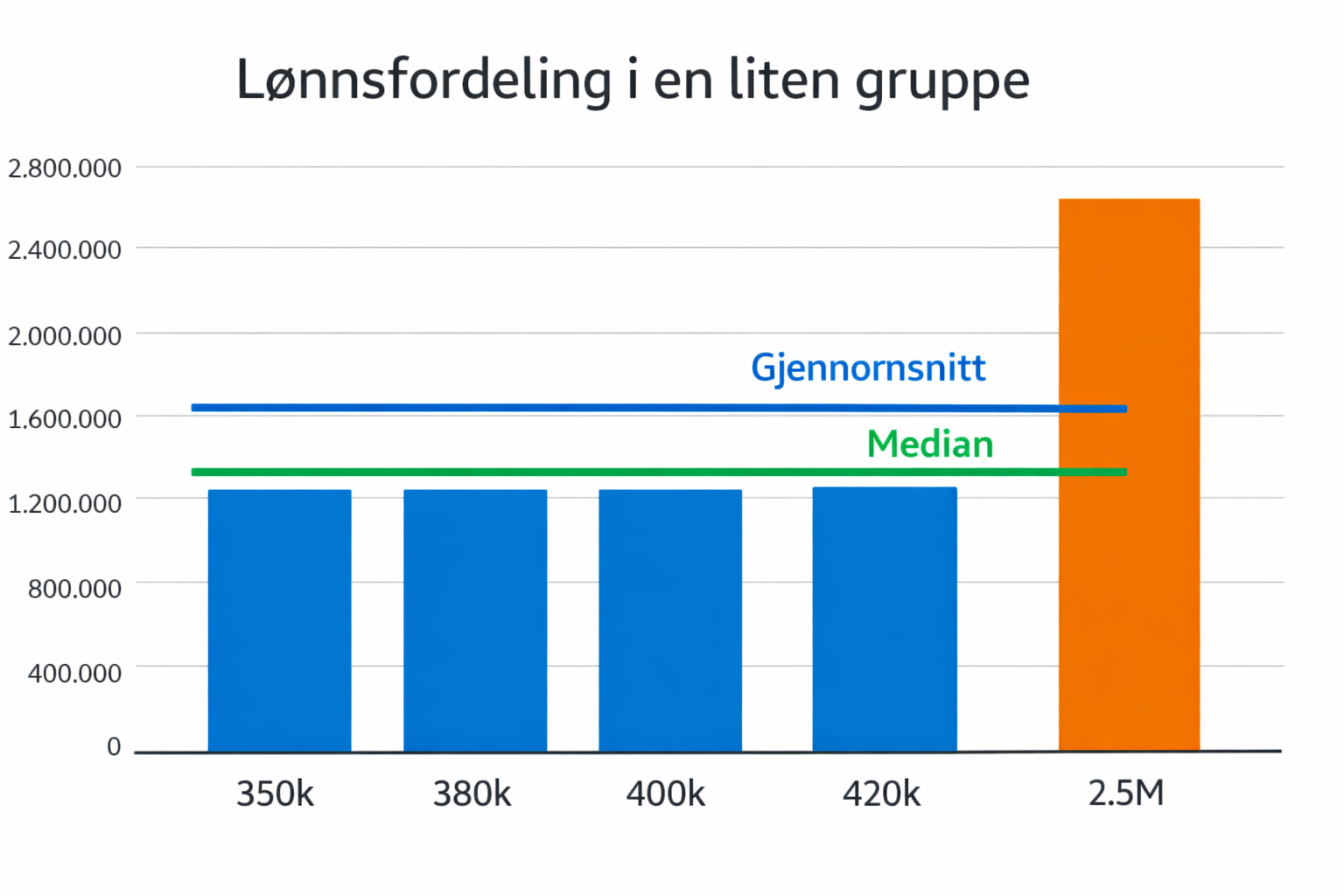
I dette eksempelet ser du fem lønninger der én er mye høyere enn de andre. Gjennomsnittet trekkes opp av det høyeste tallet, selv om de fleste tjener langt mindre.
Medianen viser midtverdien i datasettet og gir ofte et mer realistisk bilde av hva som er vanlig. Dette er grunnen til at median ofte brukes i statistikk om lønn og boligpriser.
Gjennomsnitt, median og typetall: En enkel sammenligning
Her er en rask oversikt:
Gjennomsnitt
- Tar med alle tall
- Bra når tallene er jevnt fordelt
- Kan påvirkes mye av ekstreme verdier
Median
- Midterste tall etter sortering
- Robust når datasettet er skjevt
Typetall
- Tallet som forekommer flest ganger
- Nyttig når du vil vite hva som er vanligst
Vil du lære mer om typetall? Les vår inngående artikkel her.
Tabell-blokk: Samme datasett, ulike sentralmål
Datasett: 2, 2, 2, 2, 10
| Sentralmål | Resultat | Hvorfor |
|---|---|---|
| Gjennomsnitt | 3,6 | 10 drar snittet opp |
| Median | 2 | Midterste verdi er 2 |
| Typetall | 2 | 2 forekommer flest ganger |
Dette er en rask måte å se forskjellen på.
Når bør du bruke gjennomsnitt?
Du bør ofte bruke gjennomsnitt når:
- verdiene er ganske jevne
- du ikke har store ekstreme avvik
- du trenger et samlet nivå
Akademiske skoler beskriver gjennomsnitt som et sentralmål som fungerer godt når datasettet ikke er «problematisk» med store avvik. De understreker også at datasett med likt gjennomsnitt kan være svært ulike.
Når passer median bedre?
Median er ofte bedre når:
- datasettet har ekstreme verdier
- du vil beskrive en «typisk» person
- du ser store forskjeller mellom lavt og høyt
Høyskolene har egne ressurser som bruker sentralmål på karakterer og frekvenstabeller, som nettopp viser hvorfor valg av mål betyr noe.
Hvordan regne ut gjennomsnitt i Excel og Google Sheets?
Når du har mange tall, er regneark gull.
- I Excel kan du bruke funksjonen GJENNOMSNITT.
- Eksempel: =GJENNOMSNITT(A1:A20)
Microsoft beskriver at funksjonen returnerer det aritmetiske gjennomsnittet av tall i et område.
- Du kan også bruke GJENNOMSNITTHVIS hvis du kun vil ta med tall som oppfyller et vilkår.
Microsoft beskriver at den returnerer gjennomsnitt for celler som oppfyller et bestemt krav.
Dette er nyttig hvis du vil finne gjennomsnitt for kun én gruppe. Det kan være én klasse. Det kan være ett fag. Det kan være én måned.
Mini øvelse: Test deg selv
Oppgave 1
- Tallene er: 6, 4, 5, 3, 2
- Hva er gjennomsnittet?
Tips: Legg sammen og del på 5.
Oppgave 2
- Tallene er: 1, 1, 1, 1, 9
- Hva blir gjennomsnittet, og hvorfor kan det være misvisende?
Dette trener deg i å regne, og i å tenke kritisk.
Gjennomsnitt i statistikk
I statistikk brukes gjennomsnitt for å beskrive sentrum i et datasett. Det gir et samlet bilde av nivået på tallene, og gjør det mulig å sammenligne ulike grupper eller perioder.
Samtidig brukes gjennomsnitt sjelden alene. For å forstå tallene bedre, ser man ofte på median og typetall i tillegg. Sammen gir disse målene et mer presist bilde av hvordan dataene er fordelt.
En nyttig hverdagsfunksjon
Nå vet du hva gjennomsnitt er. Du vet også hvordan regne ut gjennomsnitt. Du gjør det ved å legge sammen tallene og dele på antall tall. Dette er definisjonen av middelverdi og aritmetisk gjennomsnitt.
Du har også sett hvorfor gjennomsnitt kan bli misvisende når datasettet er skjevt. Da kan median eller typetall gi et bedre bilde. Dette er grunnen til at sentralmål må vurderes ut fra situasjonen.
Hvis du husker én ting, la det være dette. Gjennomsnitt er nyttig, men det må tolkes med hodet på.
Résumer avec l'IA :
Likte du denne artikkelen? Vurder den!
Loading...
