Matematikk har eksistert siden tidenes morgen, ifølge oppdagelsen av Lebombo-beinet som har en bavian fibula som er over 35000 år gammel. Det er kanskje den første beregningen av kalenderen eller menstrasjonssyklusen, da det er en stokk med 29 merker på. Det kan også være bevis på den første kunnskapen om primtall og multiplikasjon.
Mens matematikk kan forbli et mysterium for mange av oss, er det for matematikere et viktig verktøy til å kunne forstå og analysere verdenen vi lever i. Noen eksempler på disse verktøyene er kvadratrotregning, negative tall, differensiallikninger, brøker, eksponensiell statistikk, logaritme, komplekse tall og matematisk modellering.
Å lære matematikk krever noen ganger en viss grad av estimering, fordi det er basert på teoremer som bruker logikk. Resultatene kan beskrives objektivt som riktige selv om de er litt rare. Dette gjelder spesielt når det kommer til geometri, trigonometri, aritmetikk, algebra og kalkulus.
Hjernen vår har noen ganger problemer med å forstå mange av konseptene, men de høres ofte mer komplekse ut enn de egentlig er. Husk at det var en gang at også addisjon, subtraksjon, multiplikasjon og deling virket umulig, men ved å ta tiden til hjelp kan du lære å forstå og løse allverdens matematikkoppgaver.
I dag skal vi snakke om noen av de mest unike tallene i vår tid. Denne artikkelen vil handle om komplekse tall som 0, I, pi, det gylne snitt, primtall og perfekte tall.

Introduksjon: tallet 0 i matte
Det enkle tallet 0 har en lang historie bak seg som strekker seg over flere århundrer. Tallet ble først brukt i India og fant så veien til Europa hvor det ble utestengt av kirken i frykt for at det representerte djevelen. Det tok likevel ikke lang tid før det ble brukt av kjøpmenn på gatene, og i løpet av kort tid vokste den til tallet som vi kjenner og bruker i dag.
Hvordan null ble kjent som null
- På hindu var det kjent som Shunya,
- og ble det kjent på arabisk som Sifr.
- På latin ble det omtalt som Zephirum,
- og senere ble det norske ordet null innført.
Begrepet null har mange kulturelle, populære og filosofiske fremstillinger, deriblant inkarnasjonen av tomhet, fravær av mengde og ingenting. Tallet null er nøytralt og det eneste heltallet som ikke påvirkes av å bli multipliseres med en annen verdi.
Her er flere symboler for denne verdien:
- Mangelen på verdi (gratis),
- Fullstendigheten (100%),
- Fornyelse (derav uttrykket "starter på nytt"),
- Egget: fruktbarhet, femininitet, fosteret,
- Syklusen, osv.
Null, med sin perfekte dimensjon og form, kan sies å representere matematikkens symmetri og skjønnhet.
Introduksjon: Eulers tall
Eulers tall har 400 års matematisk historie. Tallet e er et irrasjonelt tall som skrives med et uendelig antall desimaler uten logisk sekvens. E brukes når vi vil estimere en eksponentiell størrelse.
- For eksempel forholdet 2/7 = 0,285 714 285 714 285 714...
- Blant alle desimalene etter kommaet ser man at den tilbakevendende sekvensen 285 714 er gjengitt i det uendelige.
- E er imidlertid lik = 718 281 828 459 045 235 360 287 471 352 662 497 757 247 093 699 959 57…
- Det er mer enn 800 milliarder mulige desimaler som ikke har en logisk sekvens.
Introduksjon: det imaginære tallet I
Å regne på kvadratrøttene til negative tall har ført til oppfinnelsen av komplekse tall som i. Tallet i er et rent imaginært tall som ble oppfunnet for å hjelpe forskere og matematikere med å løse ligninger når løsningen ikke eksisterte. Tallet i gjør det derfor mulig å se for seg utvinning av kvadratroten av et reelt tall: 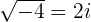
Et sett med komplekse tall anses å være en utvidelse av settet med reelle tall som inneholder et imaginært tall kalt i. Eksponent (a; b) slik at i = kvadratrot på -1 og i² = -1, med kvadratet på (-i) som -1. Prinsippet er at et hvilket som helst tall kan skrives i formen a + i b, hvor a og b er reelle, negative eller positive tall. Kvadratroten til -4 er derfor lik 2i.
- Et hvilket som helst tall i formen b i, der b er forskjellig fra 0, er et rent imaginært tall.
- Det er grunnen til at tallene "
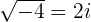 ", "
", "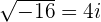 " osv., er imaginære tall.
" osv., er imaginære tall. - Hvis kvadratroten på -1 ikke eksisterer, kan vi ikke estimere eksakte eller omtrentlige desimaler slik vi gjør før røttene til positive tall (for eksempel
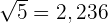 ).
). - Altså, tallet i er medlem av en enorm samling av kvadratrøtter med negative tall.
Imaginære tall er normalt pensum for r-matte og det kan være lurt å friske opp litt på kunnskapene før ditt matematikk r2 kurs.
Introduksjon: tallet Pi
Pi, også kjent som Archimedes-konstanten, er et irrasjonelt tall. Den greske bokstaven π ble valgt fra det greske navnet περίμετρος som betyr omkrets. π er symbolet for pi. Den enkle definisjonen av tallet Pi er at det er definert som forholdet mellom omkretsen (c) av en sirkel og dens diameter (d), altså c/d = pi.
Pi har blitt studert i tusenvis av år:
- Den østerriske astronomen Christine Grienberger oppdaget at pi består av 38 sifre (3.14 159 265 358 979 323 846 264 338 327 950 288 41).
- Den britiske matematikeren og fysikeren Isaac Newton og den tyske matematikeren Gottfried Wilhelm Leibniz endret beregningsmetoden og oppdaget at pi består av 15 sifre ved bruk av kalkulus' metode om det uendelige (3.14 159 265 358 979).
- I 1699 oppdaget den britiske matematikeren Abraham Sharp at pi har hele 71 sifre (3.14 159 265 358 979 323 846 264 338 327 950 288 419 716 939 937 510 582 097 494 459 230 781 64)
- Men bare noen år senere, i 1706, oppdaget den britiske astronomen John Machin at pi består av hele 100 sifre (3.14 159 265 358 979 323 846 264 338 327 950 288 419 716 939 937 510 582 097 494 459 230 781 640 628 620 899 862 803 482 534 211 706 79)
Lær om Pi og ha det gøy samtidig
Hvis du vil prøve å imponere vennene dine ved å resitere alle de 75 desimalene av π, er det flere metoder du kan bruke for å memorere dem. En av disse metodene er piems, som er enkle dikt som gjør det enklere å huske. Hvert ord i diktet representerer antall desimaler i tallrekken når de settes sammen til piems (for eksempel 'the' = 3, et ord på 10 bokstaver er 0):
- Nå trosser jeg en tenet galant (3.14159),
- Av sirkelloven: disse heltallene,
- Import av sirkler er kvotienter,
- Uhåndterlig lang serie med hjertemuskler,
- Sett alt sammen, få ingen klarhet;
- Memorering skal ikke være forbedret versjon,
- Å skape, med en tydelig takknemlighet,
- En liberal, men konformert sonett.
- Merkelig regler som jeg manipulerer,
- Gjøre det lovlig og lettere,
- Snodige tanker fra geometrisk formidler.
- Dette diktet, ubeskjedent som det er nedtrykt,
- Utviklet sammenheng - en enkel test,
- Å oppdage poesi uten tall.
Dette gir deg en samlet sum av de første 75 sifrene i pi, like enkelt som å fortelle tiden. Det setter ikke rekord med dette, men det er nok til å imponere enhver person med dine fantastiske mattekunnskaper.
Folk vil kanskje at du er matematisk begavet, inkludert medelevene og privatlæreren din. Bare vær diskret, ellers ber de deg om å løse et annet konseptuelt matematisk problem.

Introduksjon: det gylne snitt
Det gylne snitt er et irrasjonelt tall omtrent lik 1.61803, som er representert med den greske symbolet φ. Tallet skaper en veldig spesifikk ligning som utgjør det gylne snitt.
- a+b/a = a/b = φ
Med utgangspunkt i denne ligningen, kan du bygge noe som kalles den gylne spiral. Det er en logaritmisk spiral som finnes i naturen. Denne spiralen dukker opp så mye i historien, naturen og til og med i DNA-et vårt at noen matematikere tror at det gylne snitt kan være et guddommelig tall.
Introduksjon: perfekte tall
Når alle faktorer i et tall, unntatt selve tallet, legges til det tallet, blir det definert som et perfekt tall. Faktorer er tall lavere enn det tallet som kan deles i det jevnt. Et perfekt tall er et veldig sjeldent tall, og per dags dato er det bare 51 av dem funnet.
For eksempel:
- 6 er det første perfekte tallet
- 6 kan deles jevnt med fire faktorer: 1, 2, 3 og 6
- For å finne ut om 6 er et perfekt tall, legger vi sammen alle tallene som er mindre enn selve tallet: 1 + 2 + 3 = 6.
- 6 er et perfekt tall
De dukker opp på en sparsom måte over tallspekteret med 6, 28 og 496 som de eneste perfekte tallene som er mindre enn 1000. Nye tall blir oppdaget hvert år, så kanskje du finner et og lager en oversikt.
Introduksjon: primtall
Et primtall er et tall som bare kan deles (likt uten å få desimaler eller å måtte avrunde) med 1 og seg selv. 2, 3, 5, 7, 11, 13, 17, 19, 23 og 29 er eksempler på primtall.
For eksempel:
- 2 er et primtall fordi faktorene i tallet 2 er 1 og 2.
- 1/2 = 2
- 2/2 = 2
Noen fakta:
- Det eneste primtallet som også er et partall er 2
- Ingen primtall er større enn 5 slutter med tallet 5.
- 0 og 1 regnes ikke som primtall

Hvordan memorere tallsekvenser
Memorering er en enkel hukommelsesteknikk som gjør det lettere å huske ting som ellers ikke er lett å huske. Det er som et logisk spill med interaktiv matematikk som kan gjøre matte morsomt. De kan også brukes til å gjøre komplekse tall og nummersekvenser lettere å huske.
Memorering kan hjelpe deg med å lære matematikk, huske handlelisten eller telefonnumre. Det er et minneverktøy som kan hjelpe deg med matteundervisningen.
Hvis du memorerer visuelt i stedet, kan du knytte til objekter eller tegn:
- En ball for 0,
- En blyant for 1,
- En svane for 2,
- En sjøhest eller en kamel for 3,
- En seilbåt for 4
- En slange for 5
- etc.
Her er et eksempel:
- Svane, sjøhest, slange = 2, 3, 5
- Hvis du memorerer dette, vil du ha laget et fantastisk minnesystem som du kan bruke til hvilket som helst tallsekvens i matematikk.
- Du kan enten fullføre sekvensen til 100+, eller du kan si at 2 blyanter betyr 20. Du kan lage minnesystemet akkurat som du ønsker.
Et annet tips til å huske tallsekvenser, er ved å se for deg "hvor du har lagret tallsekvensen". Har du for eksempel en kode til et bankkort du trenger å huske, eks. 4747, kan du for eksempel på tastene på telefonen at du kan skrive GRIS. 4 er G, 7 er R, 4 er I, og 7 er S. Se så for deg at du står i en minibankkø, og at det står en gris foran deg og tar ut penger. Når du glemmer koden din, kan du prøve å tenke deg tilbake til den grisen som tok ut penger, og huske at gris tilsvarer koden 4747.
Å lage en studieplan som gjennom matematikken som du synes er vanskelig gradvis, vil gjøre det lettere å huske. Du kan bruke regneark, være kreativ og lage ditt eget tallsystem, løse oppgaver, ta quizzer, lære morsomme mattefakta, øve på ligningsnotasjon og mye mer. I tillegg, så kan matteundervisning på nett med en lærer hjelpe.

Tips til matematikklæring
- Gå til et matematikk-nettsted og last ned utskrivbare oppgaveark
- Lær tallmønstre på en morsom måte, f.eks gjennom piem forklart ovenfor
- Finn enkle spill for barn og jobb deg oppover mot vanskeligere nivåer
- Lage kallenavn til vanskelig emner, for eksempel Trig F. for trigonometriske funksjoner.
- Kjøp engasjerende lærebøker med mange øvingsoppgaver
- Bli med i matematikkstudiegrupper (det er gratis!)
- Se mattevideoer og øv samtidig som du ser på
- Be din matematikklærer om hva som er vurderingskriteriene for karaktersetting, og spør om hjelp til den delen du sliter med
Eksempler på vanskelige mattestykker
Noen eksempler på vanskelige mattestykker med løsninger er nevnt nedenfor:
Oppgave 1.
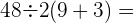
Hvordan løse denne oppgaven:
- Regn først ut parentesen:
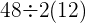
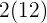 betyr det samme som
betyr det samme som 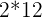 , så da kan vi regne ut følgende regnestykke:
, så da kan vi regne ut følgende regnestykke: 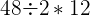
- Da blir det
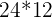 , som blir
, som blir 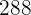
Oppgave 2.
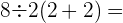
Hvordan løse denne oppgaven:
- Regner først ut parentesen og får:
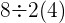
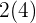 er det samme som
er det samme som 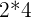 , så regnestykket er nå egentlig
, så regnestykket er nå egentlig 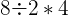
- Da får vi
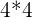 , som blir
, som blir 
Som student må du lære deg å gjenkjenne hvordan du lærer best og hvilke metoder som gir deg de beste resultatene.
Matematikkundervisning på videregående og høyere nivåer er utfordrende. Det er ikke som på barneskolen der man lærer å telle, multiplisere, dele, legge til og trekke fra. Dersom du ønsker mer hjelp med matte kan du ta mattekurs Oslo eller i andre byer. Jo mer du øver, jo større er sannsynligheten for at du vil mestre matematikkstudiene dine.
Oppsummer med AI: